补码

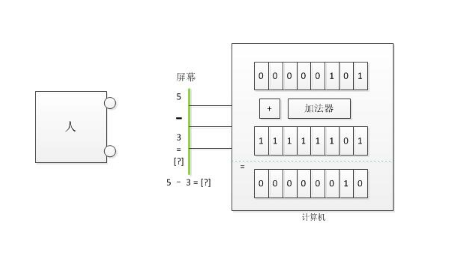
现实生活中，我们有加法、减法、乘法和除法，但在计算机中只有一个加法器。换句话说，加法运算在计算机中可以直接完成，减法、乘法和除法运算最终也得转换为加法才能实现。

数A减去数B，与数A加上"数B的补码"结果是一样的。这就是补码对于计算机的意义：将减法运算变成了加法运算。

参考

时钟

理解补码最简单的例子就是时钟。

假如一个时钟现在显示的是 10 点钟，如何将它调到 6 点钟？

答：有两种方法，一是向后拨 8 个小时，二是向前拨 4 个小时。

在这个例子中，8 和 4 互为补数，也就是说 4 的补码是 8,8 的补码是 4，而这个时钟的模就是 12。可能有人会想，在往后调 8 个小时虽然也调到了 6 点，但是他实际上比原来日期多了 12 小时。是的，的确如此，但是你的时钟有地方存储了这多余的 12 个小时吗？答案是没有，所以在你调完后，你没有记录这 12 个小时，换句话说，你把这溢出的 12 个小时自动舍弃了。当第二个人来查看闹钟时间的时候，他看到的时间就是准的。

一个数的数值是 11，他的模是 16，那么他的补码是多少？

16 - 11 = 5，即补码就是 5。

模 mod

计数系统 : 一个计数系统可以存多少容量状态的数，我叫它作为计数系统的Mod。一个计数系统不断地加一，那么它表示的数的状态也会周期性地变化，我叫这个周期的大小叫做Mod

举个两个例子：

一个包含两个 bit 的存储单位，它可以表示00，加一变成01，加一变成10，加一变成11，再加一又变成了00。即该计数系统的Mod为4
一个时钟显示十二个小时，时针旋转一周后回到原来的状态，即该系统的Mod为12

变减为加

设Mod = 16

若a=3，b=-4

则：

a + b = 3 - 4 = -1;

a + b = a + b + Mod;

a + b + Mod = a + ( Mod + b) = 3 + ( Mod - 4 ) = 15

-1 = 15; # 在计数系统中 -1 和 15 等价

Mod - 4 = 12;

4 与 Mod - 4 互为关于Mod的补数，被减数 - 减数 等价于被减数 + Mod - 减数，即 被减数 + 减数的补数。

所以，所有的减法在计算机中都可以转化为加上减数的补数，对应计算机上的概念就是补码。

使用补码运算

16 - 13，模为 32，使用补码运算该算式？

(16 + ( 32 - 13 ) ) % 32 = 35 % 32 = 3

想想看，原先是减一个数，变换后却变成了一个比减数更大的加数了，能不溢出吗。所以要模掉溢出位35 % 32。跟时钟未记录的 12 个小时是一个道理。

约定的正负号

设现有一个 4 位的计数系统，那么我们可以知道该系统的 Mod=16，即该系统一共可以表示 16 个状态。我也约定这个四位系统的 0000 状态为 0，向前连续加十六得到 0000 本身，对应表示的数字如下：

1111 = 15    0000 = 0
1110 = 14    0001 = 1
1101 = 13    0010 = 2
1100 = 12    0011 = 3
1011 = 11    0100 = 4
1010 = 10    0101 = 5
1001 = 9     0110 = 6
1000 = 8     0111 = 7

如果这个计数系统是无符号位的，显然可以知道它表示的数据范围为：0~15。如果这个计数系统是有符号位的呢？

首先要对这些数据进行分配，现在的教科书上的做法就是把 Mod 前一半划分给 0~7，后一半 Mod 划分给-8~-1，即如下图（这里二进制都是补码）:

1111 = -1    0000 = 0
1110 = -2    0001 = 1
1101 = -3    0010 = 2
1100 = -4    0011 = 3
1011 = -5    0100 = 4
1010 = -6    0101 = 5
1001 = -7    0110 = 6
1000 = -8    0111 = 7

可以看出，最高位为 0 的即是正数，最高位为 1 的即是负数。至于为什么-1 就是 1111呢？

Mod 为 16,即10000,对于1 - 1 = 0这个等式，等价于1 + (-1) = 0；即0001（二进制） + （-1）= 0000（二进制），那么（-1）= 0000 - 0001，向高位借 1 位后，减得（-1）= 1111（二进制），所以计算机中使用1111来表示以及存储-1。

无符号数

无符号数强制转换为有符号数: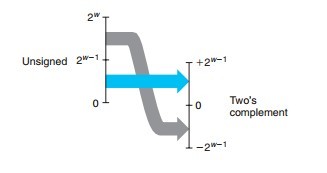

有符号数强制转换为无符号数: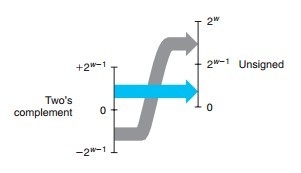

#include <stdio.h>
int main(){
    char t = 0xFF;
    unsigned char u = 0xFF;
    printf("t=%d u=%u\n",t,u);
    printf("t2u=%u u2t=%d\n",(unsigned char)t,(char)u);
}
// t=-1 u=255
// t2u=255 u2t=-1