深入理解计算机系统
第一部分: 1 ~ 6 , 帮助我理解了程序和硬件之间的交互关系。
第二部分: 7 ~ 9 , 帮助我理解了程序和操作系统之间的交互关系。
第三部分: 10 ~12 , 帮助我理解了与I/O设备以及其他程序通信,理解了网络服务程序和并发程序。
进程
系统保持跟踪进程运行所需的所有状态信息,这种状态称为“上下文”,它包括了程序计数器PC、各个寄存器、使用到的内存。在任一时刻,一个处理器只能执行一个进程的指令。
当系统决定将控制权从当前进程转移到另一个进程时,就会进行“上下文切换”,即保存当前进程的“上下文”,然后加载别的进程的“上下文”。

虚拟内存
虚拟内存为进程提供了一个假象,即每个进程都在独占内存,每个进程看到的都是一样的存储器,称为虚拟地址空间
每个进程看到的虚拟地址空间由准确定义的区组成,每个区都有专门的功能
程序代码区:对所有进程来说,代码是从同一固定地址开始
C全局变量区:紧邻着程序代码区,存储的的是初始化的数据
堆:紧邻着全局变量区,可以动态扩展使用的内存,使用malloc申请,free释放
共享库:存在虚拟地址空间中间,存放的是c标准库
栈:位于用户虚拟地址空间顶层(它的上面是内核虚拟地址空间,是不允许用户操作的),编译器使用它来实现函数调用,函数调用,栈增长,函数返回,栈消退
内核虚拟存储器:位于整个虚拟存储器顶部,是为内核保留的,不允许应用程序读写和直接调用内核代码定义的函数
文件
文件就是字节序列,仅此而已。每个IO设备,磁盘、键盘、显示器、网络,都可以看成是文件。
文件向应用程序提供了一个统一的视角,来看待系统中各式各样的设备,例如,处理磁盘文件内容,无需了解具体的磁盘文件,同一个程序就可以在使用不同磁盘技术的不同系统上运行。
2. 信息的表示与处理
整数
对于整数,使用有限位来编码的方式进行表示。并且区分了两种编码:有符号编码、有符号编码(也称为补码编码)。
自然数字 有符号编码 无符号编码
0 0000 0000 0000 0000
-1 1111 1111 无编码
-2 1111 1110 无编码
1 0000 0001 0000 0001
2 0000 0010 0000 0010
130 溢出错误 1000 0010 有限的位只能表示有限的整数,所以当运算结果超出了表示范围,就会触发CPU产生溢出错误中断。
例如32位下200*300*400*500的计算结果是-884901888,产生一个负数结果原因就是运算结果超出了32位能表达的正数范围。
C语言中,32位与64位下的数据类型占用的字节大小有些许不同,long与*类型在64位系统下,都是占用8个字节。

大端法与小端法
数据 0x01234567 在内存中的存储情况:
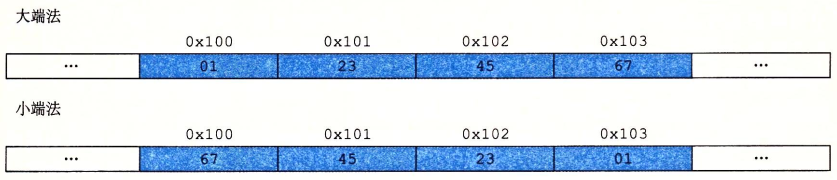
C语言中,需要关注字节顺序的三种情况:
网络传输,网络传输规定使用大端法,所以在上传数据时,需要转化为大端顺序,在接收数据时需要转化为本机字节顺序
第二个是在阅读反汇编语言时,比如

第三个是在使用强制类型转换,显示
struct和union中内容时
Sun是大端机,所以同样的数据12345在内存中存储和其他机器不一样:

对于字符串来说,则没有字节顺序的问题,因此,文本数据比二进制数据更具有平台独立性。
const char *s = "abcdef"; // 在任何系统的存储都是: 0x 61 62 63 64 65 66 00移位运算
左移: 丢弃最高位,然后向左移动,不足位数补0。
右移:
无符号数: 丢弃最低位,然后向右移动,左边补0。(逻辑右移)
有符号数: 没有统一,大多数编译器采用算术右移,即根据有符号数的正负来决定,左边是补0还是补1,极个别编译器采用逻辑右移
除 C 语言外,很少有语言支持无符号整数,它带来的漏洞比它带来的好处(多了一倍可用的正数)更多。因此,Java 被设计成只支持有符号整数,并且规定底层使用补码来实现。>> 被定义成算术右移,>>> 被定义成逻辑右移。

使用数学语言描述整数

二进制转无符号数:


二进制转补码(有符号数):
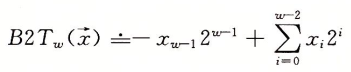

由此我们可以计算出 N位 二进制可以表示的数的范围:

强制类型转换
无符号数与有符号数(补码)相互转换的基本原则:底层的二进制数不变。
有符号数(补码) 转 无符号数计算如下:

short int v = -12345;
unsigned short uv = (unsigned short) v;
printf( "v = %d, uv = %u" , v , uv ); // v = -12345 uv = 53191反过来,无符号数转有符号数(补码)计算如下:

如果通过画图来形象化,表达这种计算,如下:

C语言中,执行一个运算时,如果操作数既有无符号数,又包含有符号数(补码),那么通常是(隐式地)将 有符号数(补码) 解释为 无符号数 然后进行计算。如果算术操作,因为无符号数 与 有符号数的 底层 二进制计算逻辑都是一样的,所以不会有问题。
但是,如果是 < 和 > 这样的比较操作,则会引发下面问题:

打*的求值结果是错误的,原因就是:有符号数 隐式地解释成了无符号数(补码),所以负数被解释成了一个非常大的正数,所以<操作得出了一个 对人类来说 ,是错误的结果。
下面都是由于隐式转换和无符号类型带来错误的经典代码:
float sum_elements( float a[], unsigned lenght ){
int i;
float result = 0;
// 当 length 传入 0 时,由于是无符号数,length - 1 的结果是一个很大的正数
// 结果会导致,a[i] 访问非法内存
for( i = 0; i <= length - 1; i++ )
result += a[i];
return result;
}// size_t 的定义是 unsigned int
size_t strlen( const char *s );
int strlonger( char *s, char *t ){
// 两个无符号数相减,结果恒定是 >= 0 的,当 t 更长时,这个函数的返回是不符合期望的
return strlen(s) - strlen(t) > 0;
}void *memcpy( void *dest, void *src, size_t n );
#define KSIZE 1024
char kbuf[KSIZE];
int copy_from_kernel( void *user_dest, int maxlen )
{
int len = KSIZE < maxlen ? KSIZE : maxlen; // 如果 maxlen < 0, 则 len 取值为 maxlen (负数)
// memcpy 中 len 的声明为 size_t, 所以 len(负数) 被解释为一个很大的正数,将导致拷贝内核中的不该被用户访问到的内存
memcpy( user_dest, kbuf, len);
return len;
}PS: 无符号数为程序带来了隐藏的非常深的错误,JAVA语言设计中去掉了无符号数编码,统一只采用有符号数(补码)真的是明智之举,而C++语言还沿用了这样的错误设计,诶。。。
低位数向高位数转换
short sx = -1234;
int x = (int) sx;对于无符号数,直接补0。
有符号数:
正数,补0
负数,补1
自然数 char -> short
139 1000 1011 0000 0000 1000 1011 (无符号编码)
11 0000 1011 0000 0000 0000 1011 (有符号编码)
-81 1010 1111 1111 1111 1010 1111 (有符号编码)高位数向低位数转换
int x = 53191;
short sx = (short) x;
int y = sx;将 x 强制转换为 short 时,C语言就将32位的 int 截断成为了 short,截断就是 丢弃高位的 过程,必然会带来数据的损失。所以,建议是 绝不作这种操作。
整数的算术运算
无符号数的加法:

有符号数(补码)加法:

无符号数求相反数:

有符号数(补码)的相反数:

无符号数与有符号数的相反数求法的底层逻辑都是一样的,都可以使用取反再加1这个操作,取得二进制数,然后再以有符号数或补码解释。
PS: TMin 的相反数 是它本身,所以TMin经常是一个函数的边界条件,或是例外情况,如下例:
// 有符号数 , 加法溢出判断
int tadd_ok( int x, int y )
{
int s = x + y;
// 两个正数相加,结果小于 0,正溢出
if( x >= 0 && y >= 0 && s < 0 )
return 0;
// 两个负数相加,结果大于 等于0, 负溢出
if( x < 0 && y < 0 && s >= 0 )
return 0;
return 1; // 无溢出
}
// 当 y 取 TMin 时, -y 也等于 TMin
// 期望情况: x为正数: 19 - (-128)) 溢出 0; x 为负数: -19 - (-128) 不溢出 1
// 实际情况: 根据 tadd_ok 的逻辑,x为正数时,返回 1; x 为负数时,返回 0 正好相反。
int tsub_ok( x, y ){
return tadd_ok( x, -y );
}
在补码编码下,要快速对一个数进行求反操作,可以使用这个技巧 所有位取反再加1:

通过这个技巧,在已知一个自然数的补码的情况下,比如 5的补码编码为0101,可以很快求出该数的相反数 -5 的补码为 1011。
无符号数乘法:

有符号数(补码)乘法:

举例说明两种乘法的结果: 3位无符号和补码的乘法示例,虽然完整的乘积的位级表示可能会不同,但是截取到3位后,位级表示是相同的

算术运算的溢出
无符号数 + 无符号数:
无符号数 + 有符号数: 其中的有符号数会 隐式地 转换成 无符号数,然后再进行运算
// 检测无符号数相加,是否会发生溢出
int uadd_ok( unsigned int x, unsigned int y )
{
unsigned int s = x + y;
return s >= x; // 如果无溢出,s 一定大于或等于 x 或 y
}有符号数 + 有符号数:
乘法溢出:
void* copy_elements( void *ele_src[], int ele_cnt, size_t ele_size )
{
// 下行 如果 ele_cnt * ele_size 发生乘法溢出,缓冲区分配大小 与 实际需要的不符
void *result = malloc( ele_cnt * ele_size );
if( result == NULL )
return NULL;
void *next = result;
// 此处的 循环就会,导致数据复制到缓冲区之外的地方,破坏其他数据结构
for( int i = 0; i < ele_cnt; i++ )
{
memcpy( next, ele_src[i], ele_size );
next += ele_size;
}
return result;
}// 检测 32 位 乘法溢出
int tmult_ok( int x, int y )
{
// 这里的强转换很重要,没有的话,可能会先用32位计算,然后拓展到64位
int64_t pll = (int64_t) x * y;
return pll == (int)pll;
}浮点数
浮点数的编码与实现是与整数完全不同的。
它最大缺点在于精度有限,会带来一些计算错误,比如(3.14 + 1e20) - 1e20的计算结果是0.0,而3.14 + (1e20 - 1e20)的结果是3.14,正是由于精度问题,1e20是一个非常大的数,加上3.14也没有可以表示它们的位。

小数转换成浮点数

3. 机器代码
目标: 能阅读和理解编译器产生的代码。
(gdb) x/14xb multstore # 打印 函数 multstore 地址处的 14 字节的内存
理解指针
缓冲区溢出
// 从标准输入获取字符串
char *gets( char *s )
{
int c;
char *dest = s;
while( (c = getchar() ) != '\n' && c != EOF )
*dest++ =c;
if( c == EOF && dest == s )
return NULL;
*dest++ = '\0';
return s;
}
void echo()
{
char buf[8];
gets(buf); // 当标准输入 超过 8 个字符时,就会发生缓冲区溢出
puts(buf);
}如下图,当buf被填入过长的字符串时,会依次破坏echo、返回地址、调用者的栈。导致函数返回时,PC程序计数器会指向一个未知的返回地址,就发生了缓冲区溢出,如果有人利用这个将PC指向一段攻击系统的指令,就是缓冲区溢出攻击。


对抗缓冲区溢出攻击
栈基址随机化(ASLR 地址空间布局随机化技术)
// 每次程序运行,可以发现 local 的地址都是不同的
int main(){
long local;
printf( "local at %p\n", &local );
return 0;
}栈破坏检测
最近的GCC版本中,加入了一种 栈保护机制 , 原理是: 在局部缓冲区与栈状态之间存储一个 金丝雀值,它是程序每次运行随机产生的,所以攻击者不知道它的值,函数调用后,在返回之前 使用代码 检查这个金丝雀值是否被改变,如果被改变了,则终止程序。

echo:
.LFB39:
push rbx
sub rsp, 16 ; 产生 金丝雀 值
mov rax, QWORD PTR fs:40 ; 设置 金丝雀 值
mov QWORD PTR 8[rsp], rax
xor eax, eax
mov rbx, rsp
mov rdi, rbx
call gets@PLT
mov rdi, rbx
call puts@PLT
mov rax, QWORD PTR 8[rsp]
xor rax, QWORD PTR fs:40 ; 对比 金丝雀 值
jne .L5
add rsp, 16
pop rbx
ret
.L5:
call __stack_chk_fail@PLT ; 终止程序这种金丝雀代码是GCC默认会产生的,使用-fno-stack-protector来阻止GCC产生这种代码。
限制可执行代码区域

4. 指令体系结构
处理一条指令包括很多操作,将它们组织成某个特殊的阶段序列,即使指令的动作差异很大,但所有的指令都遵循统一的序列:
取指 : 读取指令字节
译码 : 根据指令,读取操作数
执行 :
访存 : 将数据写入内存
写回 : 将结果写入寄存器
更新PC :
指令执行过程示意图,沿着顺时针循环这个过程:

5. 优化程序性能
6. 存储器层次结构
7. 链接
.o文件格式:

ELF可执行文件格式: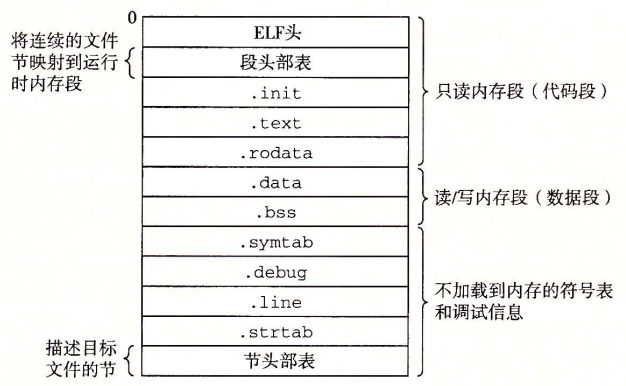
8. 异常控制流
9. 虚拟内存
虚拟内存是硬件异常、硬件地址翻译、主存、磁盘文件和内核软件的完美交互,它为每个进程提供了一个巨大的、一致的和私有的地址空间。

MMU 内存管理单元: CPU上的专用芯片,利用存放在主存上的查询表来动态翻译虚拟地址,该表的内容由操作系统管理。
虚拟页VP: 有三种状态,未分配(不占磁盘和主存)、未缓存(不占主存)、已缓存(占用主存)
物理页PP:
页表:
操作系统为每个进程,提供一个独立的页表,因而也就是一个独立的虚拟地址空间。

虚拟地址 与 物理地址 的翻译

页面命中时,完全由硬件实现所有步骤;如果缺页,则需要硬件和操作系统内核协作完成:

虚拟内存 结合 高速缓存的实现如下,地址翻译发生在高速缓存查找之前:

程序直接使用存储器的缺点
进程太多,存储器不够程序使用的
进程间互相不小心篡改彼此的内存数据,进程可能崩溃
它将内存 看作是存储在磁盘上的地址空间的 高速缓存,在内存中只保留活动的进程,并且根据进程的切换在磁盘和内存之间来回交换数据
它为每个进程提供了一致的地址空间,从而简化了存储器管理
它保护了每个进程的地址不被其他进程破坏
可以创建或者销毁储存器片 chunk
可以将存储器片映射到磁盘文件的某个部分,比如你可以通过读写存储器来修改一个磁盘文件的内容,再比如可以不需要显示拷贝,就可以加载一个文件的内容到存储器中
进程之间也可以共享某块存储器片
物理和虚拟寻址
物理地址:计算机内存被组织成一个连续的数组,每个字节都有一个唯一的物理地址
物理寻址:早期的PC是物理寻址的,cpu产生一个物理地址,通过存储器总线传递给主存,主存将该物理地址处的数据取出给CPU,CPU会把数据放在寄存器里
虚拟寻址:现在计算机cpu产生一个虚拟地址,这个虚拟地址经过cpu里面的 存储器管理单元 (Memory Management Unit,MMU)专用硬件的翻译,变成物理地址,然后传给内存
地址空间
地址空间: 非负整数的有序集合 {0,1,2,3,4,5...} , 2的n次方个元素,称为地址空间大小
虚拟地址空间: cpu从2的n次方的地址空间生成虚拟地址,称为虚拟地址空间
物理地址空间: 与系统物理存储器的内存大小对应,有多大的内存就有多大的地址空间
数据对象(字节)与地址的区别: 两者是不同的, 一个内存里的字节可以有多个地址与之对应,比如主存中每个字节都有一个虚拟地址空间的虚拟地址和一个物理地址与之对应